Interpretation of Clafers, Model, and Instances

When modeling in Clafer, we are building a model which describes model instances. A model consists of clafers, constraints, and objectives and a model instance consists of clafer instances and values. There are never instances in the model, only instance specifications from which instances are produced either manually or by an instance generator.

During modeling, we assign some interpretation to clafers and their instances.

For example, when performing feature-oriented domain analysis (FODA), we interpret a clafer model as a feature model, clafers and features, feature groups, and attributes; and we interpret model instance as a feature configuration. For more information on using Clafer for feature modeling, see Feature Modeling using Clafer.

When modeling concepts, we can interpret clafer models as abstractions and examples, clafers as concepts and properties, and clafer instances as data.

Finally, when modeling architecture, we can interpret clafers as various architectural concepts, such as, analysis functions, functional devices, connectors, devices, architectures, deployments, etc. For more information on using Clafer for architecture modeling see Alexandr Murashkin’s MMath thesis.

Structure of a model in Clafer: hierarchy of clafers

Clafers and constraints form a hierarchy expressed through indentation. Constraints are stated between square brackets: [ and ]. Both clafers and constraints need to be declared in a new line. We describe our terminology related to the clafer hierarchy below.

A
  B ?
    C ?
    [ ... ]
  D ?
  [ ... ]
<< max ... >>
<< min ... >>

Parent is a direct ascendant and child is a direct descendant. Constraints are said to be placed in context of a clafer meaning that they apply to every instance of that clafer. Constraints cannot have any descendants.

Note: The square brackets [ and ] are part of the syntax of a constraint and they do not play the traditional grouping role of round- ( ) and curly- { } brackets. The nesting of the opening square bracket [ determines the context of the constraint. The following is an incorrect example:

A
   B [
   ...
   ]

In the example below, the placement of the constraint significantly affects its meaning:

A
  [ # C > 5 ]
  B +
    C +
    [ # C > 5 ]

In general, every constraint can be pulled up by adding explicit quantification. The following four models are semantically equivalent; however, proper constraint nesting contributes to readability and model conciseness. In the fourth model, the constraint is pulled to top-level.

A *
  B *
     C *
        [ Phi ]

A *
  B *
     C *
     [ all x : this.C | Phi ]

A *
  B *
     C *
  [ all x : this.B.C | Phi ]

A *
  B *
     C *
[ all x : A.B.C | Phi ]

In the constraints above, this refers to an instance of the context clafer of the constraint. That is, in model #2, this refers to an instance of B, in #3, an instance of A, and in #4, this is not used because the constraint is top-level.

For convenience, a single constraint can be written in multiple lines and it means the conjunction of the constraints from each line. The following three models are equivalent:

A
  B ?
  C -> int ?
  D ?
  [ B
    C = 10
     ! D ]

A
  B ?
  C -> int ?
  D ?
  [ B ]
  [ C = 10 ]
  [ ! D ]

A
  B ?
  C -> int ?
  D ?
  [ B && C = 10 && ! D ]

Inheritance hierarchy

Unlike the nesting hierarchy of clafers, the inheritance hierarchy is not directly visible in the model. We describe our terminology related to the inheritance hierarchy below.

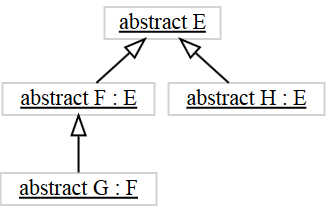
abstract E
abstract F : E
abstract G : F
abstract H : E

Any clafer can have at most one direct super clafer.

We provide a graphical visualization of the inheritance hierarchy:

Meaning of a model

Any clafer can be thought of as a form that describes many instances. Constraints restrict the set of instances described by a given clafer. Sometimes, a clafer becomes so restricted that it describes a set of isomorphic instances.

Important note for programmers: Clafer is a declarative language and a clafer model is a declarative specification. There are no classes, fields, attributes, objects, assignments, references, nulls in Clafer. An abstract clafer declaration defines a new type. A concrete declaration additionally defines a relationship between the clafer and its parent, a set of instances of the clafer and instances of all of its descendant clafers. In our example, the model about a Person contains a clafer declaration in each line.

abstract Person
  Name -> string
  xor Gender
     Male
     Female
  Married ?
  Address
    Street -> string
      UnitNo -> integer ?
  
JohnDoe : Person
  [ Name = "John" ]
  [ Male ]
  [ Married ]
  [ Street = "12 Main St." ]
  [ UnitNo = 3 ]

In general, to declare a new clafer, simply state its name and indent it appropriately with respect to some other clafer. Clafers that are not indented are the root clafers (or top-level clafers).

Declarations of clafers can additionally be extended with:

• Type, that is, a kind of value a given clafer can point to: string, integer, or any other clafer, e.g.,

Name -> string
Country -> NorthAmericanCountry

Note: Reference clafers can only point to root (top-level) clafers. This restriction is relaxed in the upcoming Clafer 0.4.0 which implements redefinition.

• Clafer cardinality, that is, how many instances of a given clafer can appear as children of the parent clafer: ? (optional = 0 or 1 instance), nothing (default) (mandatory = exactly one instance), * (multiple optional = any number of instances), + (multiple mandatory = at least one instance), m..n (minimum m and maximum n instances), and n (exactly n instances), e.g.,

UnitNo -> integer ?	 
City -> string		 
child -> Person *     
participants -> Person + 
hand 2			 
doors 3..5		 
flavour 2..*	         
LochnessMonster  0	 

• Group cardinality, that is, how many of the children of a given clafer can be instantiated: any (no restriction – any number, same as 0..*), xor (exactly one of the children clafers, same as 1..1), or (at least one of the children clafers or more, same as 1..*), mux (at most one of the children clafers, same as 0..1), and m..n (at least m, at most n of the children clafers), e.g.,

Address
  Street -> string 
  City -> string
0..* Address2
  Street -> string
or Gender
  Male
  Female 
xor MaritalStatus
  NeverMarried
  Married
  Divorced 
mux Title
  Mr
  Mrs
  Ms 
2..3 Flavour
  Strawberry
  Chocolate
  Vanilla	 

Important! Clafers grouped under a clafer with group cardinality other than any (0..*) by default have optional clafer cardinality. E.g., Male, Married, Ms, and Strawberry are optional. Children of Address and Address2, however, have the default clafer cardinality – mandatory (1).

• Direct super clafer. Clafers can inherit children of other clafers, e.g.,

JohnDoe : Person 
abstract Student : Person 

In both examples above, Person is a direct super clafer. Only root (top-level) clafers can be direct super clafers (This restriction is lifted in Clafer 0.4.0 which supports both references to and inheritance from nested clafers).

• Abstract or concrete. Abstract clafers represent forms based on which concrete clafers can be constructed. However, abstract clafers do not directly represent a set of instances. Concrete clafers represent sets of instances, with cardinality of that sets being the same as the cardinality of the clafer. Only concrete clafers can be referenced (pointed to by other clafers) within the constraints, e.g.,

abstract Person  
JohnDoe : Person  
TeamMember : Person 10 

The difference between : and ->

Both : and -> are different means of defining subsets. Colon : defines a partitioning, that is, a division of a set into disjoint and covering subsets; whereas, reference -> defines an arbitrary subset of instances of the given cardinality, potentially overlapping with existing partitions. For example,

abstract Person 
Alice : Person 
Bob : Person 
Member : Person 5

defines a partitioning of the set Person into 7 disjoint and covering subsets (Alice and Bob are singletons and Member has 5 elements). However,

pair -> Person 2

defines an arbitrary subset of the set Person of cardinality 2. Example instances of pair include

pair = Alice, Bob 
pair = Alice, Member1 
pair = Member2, Member5

Desugaring

So far, we have been using the “concise” Clafer notation that leverages many convenient defaults. The Clafer translator can output a fully resolved “desugared” model in full Clafer syntax. The desugared model is useful for learning what the different defaults are expanded to.

Usage: Invoking the translator as follows

clafer –m=clafer <model_name.cfr>

will produce a new file model_name.des.cfr.

Both the concise and the desugared versions of the person model used throughout this tutorial are available: person.cfr and person.des.cfr. Here let’s look at the desugaring of a contrived example. Fragments in green and bold are the same in both models. Fragments in red and bold on the left are expanded into corresponding fragments on the right. Fragments in black on the right are results of applying defaults, resolving indentation, and making the identifiers unique.

In the desugared model, the following changes were made:

• Names were mangled to be unique (note that a new clafer B is declared as a child of N and it’s unique name is different from the clafer B declared as a child of A)
• Indentation was resolved into explicit nesting using curly brackets { }
• Clafer and group cardinalities were specified explicitly
• The default super clafer clafer was added
• The multi-line constraint was rewritten into an explicit conjunction
• The default qualifier some was added in the last constraint

The distinction between the concise and desugared syntaxes is not strict – modelers may choose the level of detail that is most suitable for their purpose. For example, explicit nesting using { } may be freely mixed with indentation. Also, modelers may choose different styles of specifying cardinality, for example, one may interchangeably use 0, 1, 1..1, ?, 0..1, +, 1..*, *, 0..1, etc.

Exercise - Modeling a Concept

Back Introduction