Directed Graph Reachability in Presence of Variability

Metamodeling a directed graph

We can model a directed graph with non-zero weighted edges as follows:

That is, every node can be connected to zero or more other nodes and multiple edges in the same direction are allowed between any two nodes. To only allow at most one edge in the same direction between any two nodes, one would use a set-valued reference: abstract Edge -> Node *.

We compute total weight of all edges present in a graph as follows:

Modeling a concrete graph

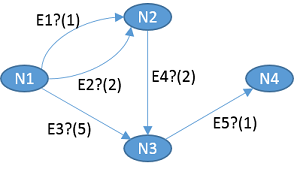
Then, we can specify a concrete graph in which every edge is optional shown below. The optionality of the edges is indicated using question marks, and the weights are shown in parentheses.

We model the example graph in Clafer directly as follows. Note, that we are refining the original reference clafer Edge:

• ->> (bag) into -> (set),
• * into ?, and
• type Node into the specific nodes (N1, N2, etc.)

Expressing reachability constraint

Now, we would like to express a constraint that the node N4 must be reachable from N1. That is not currently possible in Clafer 0.4.1; however, as of 0.4.1 we can use Alloy escapes to write the constraint directly in Alloy. Markers [alloy| and |] indicates the beginning and the end of embedded Alloy code.

[alloy|
fact {
    c0_N4 in c0_N1.^(r_c0_Edge.c0_Edge_ref)
}
|]

The expression r_c0_Edge.c0_Edge_ref computes a relation Node->Node, so that we can compute a transitive closure of that relation and thus express the reachability constraint.

When writing Alloy code in the escapes, we have to use names from the Alloy output generated by Clafer compiler. A simple rule is that whenever a name of a clafer is unique, it will always be prefixed with c0_ in the Alloy output. Non-unique clafer names have prefixes c0_, c1_, …, assigned in the order of the appearance of the clafers in the model.

For reference, here’s the relevant Alloy output generated for clafers Node and Edge:

abstract sig c0_Node
{ r_c0_Edge : set c0_Edge }

The field r_c0_Edge is a relation c0_Node->c0_Edge.

abstract sig c0_Edge
{ c0_Edge_ref : one c0_Node }
{ one @r_c0_Edge.this }

The field c0_Edge_ref is a relation c0_Edge->c0_Node. Thus, the composition r_c0_Edge.c0_Edge_ref is a relation Node->Node.

In ClaferIDE, you can see the Alloy output in the Compiled Formats window by selecting Alloy Model:

Playing with the model

Use ClaferIDE with the Alloy-based backend to see all graphs in which the node N4 is reachable. The Choco-based backend does not yet support nested abstract clafers but one can already escape into chocosolver’s JavaScript using the [choco| … |] escape.

Tip: in IDE, you can keep the ClaferIG session running but you must click on Compile button after each change to the model. ClaferIG will then reload the session and keep all settings, such as, scopes and bitwidth.

1. Can you make N1 prohibited (that is give it cardinality 0) and get an instance? Why?

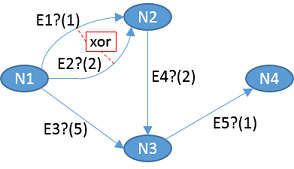
2. Make the edges E1 and E2 mutually exclusive. You can use the xor operator. We would like to obtain a graph which can be visualized as follows:

• Can you make N1 optional and get an instance without N1? Why?

3. Make the node N2 prohibited and see what happens. Is that what you expected? Why aren’t there more instances?

4. Make the node N2 optional (that is give it cardinality ?) and see what happens. Is that what you expected?

   • Then add a constraint [no N2].

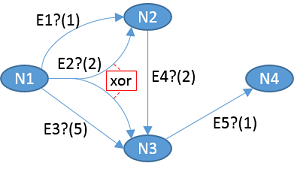
5. Make the edge E2 point to either N2 or N3. We would like to obtain a graph which can be visualized as follows:

Note that this case is different from point 2, where we have two different edges which are exclusive. Here, we have a single edge which can have different targets.

See answers to these questions at the end of page.

Model summary

Finally, here’s a summary of our model. Double click on the graph to show/hide references.

Our example graph is actually visible in the graphical rendering of our model. Why? Only because we used reference refinement and we specified the targets of edges as types of the references. That made this information available statically. Had we used constraints to specify the targets of the edges, this information could only be obtained by constraint solving and it would be different for every instance. Thus, using reference refinement makes more structure statically visible compared to using constraints from which such structure is hard to recover.

Answers to the questions

1. No. The reachability constraint requires N4 to be in a set of nodes reachable from N1. If N1 is empty, so is the set of reachable nodes, and so N4 cannot be in an empty set.

2. The constraint can be written as [E1 xor E2].

• No, if the constraint is nested under N1. In this case, ignoring the reachability constraint, the xor means that exactly one of E1 and E2 must be present. For that to be true, N1 must always be present because the edges are nested under nodes and E1 and E2 cannot exist without their parent node N1. To mitigate that, we could also nest the constraint under N1, so that the constraint only must hold when an instance of N1 is present:

N1 : Node
    [E1 xor E2]
...

3. Because N2 is not present, there cannot be any edges incoming to or outgoing from N2, which leaves only one possible path via E3 and E5.

4. Yes. Graphs both with or without N2 are possible. Adding the constraint no N2 is equivalent to making N2 prohibited as in point 3.

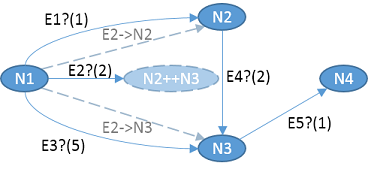
5. The idea that an edge points to either N2 or N3 can be formalized by introducing an derived sum node N2++N3 which represents the union of the two nodes. Such a derived node can then be used as a target of E2.

Also, observe that we now have two derived projections of E2 called E2->N2 and E2->N3, which illustrates the possible concrete edges in a resulting graph.

Concretely, specify the target type of the edge E2 as N2 ++ N3, that is, E2 : Edge -> N2 ++ N3 ?. Observe that the edge is still optional, meaning there will be at most one instance of E2 in the model. The type specifies the set of valid values from which at most one can be taken due to the cardinality. That is significantly different then specifying a constraint

E2 -> Node 2
[ E2 = N2 ++ N3 ]

Constraints are expressed over instances and this constraint specifies there will be two instances of the edge E2, such that E2$1 = N2 and E2$2 = N3.